Vạn Dặm Cúc Họa Mi – Been trying to look for some examples with no luck all I found is related to square roots, not cube roots Anyway I'm trying to solve lim n → ∞ n 1 3 − n 3 The limit is obviously 0= lim n→∞ 3 n1 = 0 < 1, Thus, the series P 3n n!

Exercise 02 Studocu
The value of lim_(n rarr oo)(1+2+3+...n)/(n^(2)+100) is equal
The value of lim_(n rarr oo)(1+2+3+...n)/(n^(2)+100) is equal-IIT JEE 12 Determinants 5 If the sum of n terms of an AP is given by S n = n 2 n, then the common difference of the AP is KCET 6 The locus represented by x y y z = 0 is KCET 18 Three Dimensional Geometry 7 If f (x) = sin − 1 ( 2 x 1 x 2), then f' ( 3) isLimits to Infinity Calculator Get detailed solutions to your math problems with our Limits to Infinity stepbystep calculator Practice your math skills and learn step by step with our math solver Check out all of our online calculators here!




Geneseo Math 222 01 Absolute Convergence
Giới hạn lim (((2^(n 1)) ((35)^n) 5))((((32)^n) ((95)^n)))bằng?Limits of Sequences, Lim We already know what are arithmetic and geometric progression a sequences of values Let us take the sequence a n = 1/n, if k and m are natural numbers then for every k m is true a k > a m, so as big as it gets n as smaller is becoming a n and it's always positive, but it never reaches null In this case we say that 0 isL t n → ∞ 1 3 2 3 n 3 1 n 2 2 (n − 1) 2 3 (n − 2) 2 n 1 2 equals to View solution The value of x → 1 lim x − 1 x x 2 x n − n is
Lim 3−2n4n2 4n25n−3 lim 3 − 2 n 4 n 2 4 n 2 5 n − 3 có giá trị là bao nhiêu?Limit Comparison Test Example n (n 2 1) 1 n n2 1 We have, un = 2 , let us take vn = 2 = 3 By p – series test vn is convergent n 1 n n2 𝑢𝑛 Now, lim 𝑛→∞ 𝑣𝑛 n /(𝑛21) = lim 3 𝑛→∞ 1/𝑛2 n = lim x ( n )3 𝑛→∞ 𝑛2 1 𝑛2 = lim 𝑛→∞ 𝑛2 1 𝑛2 /𝑛2 = lim 𝑛→∞ 𝑛2 /𝑛2 1/𝑛2 1 Get an answer for 'Calculate the limit n^2/( 1 2 3 n ), x>infinity' and find homework help for other Math questions at eNotes Search this site Go iconquestion
Solutions page 3 of 7 MAT V1102 – 004 14 Since n!Watch Video in App This browser does not support the video element 2147 k 25 k Answer Step by step solution by experts to help you in doubt clearance & scoring excellent marks in(a) lim n→∞ (n1)z2n2 nz2n = z 2 =⇒ R = 1 (b) lim n→∞ 4 n1z3 3 4nz 3n = 4z3 =⇒ R = 1 41/ (c) lim n→∞ √ n1zn1 √ nzn = z =⇒ R = 1 3 Find closed form expressions for the following series (a) X∞ n=1 nzn (b) X∞ n=0 (−1)n zn (2n1)!



2
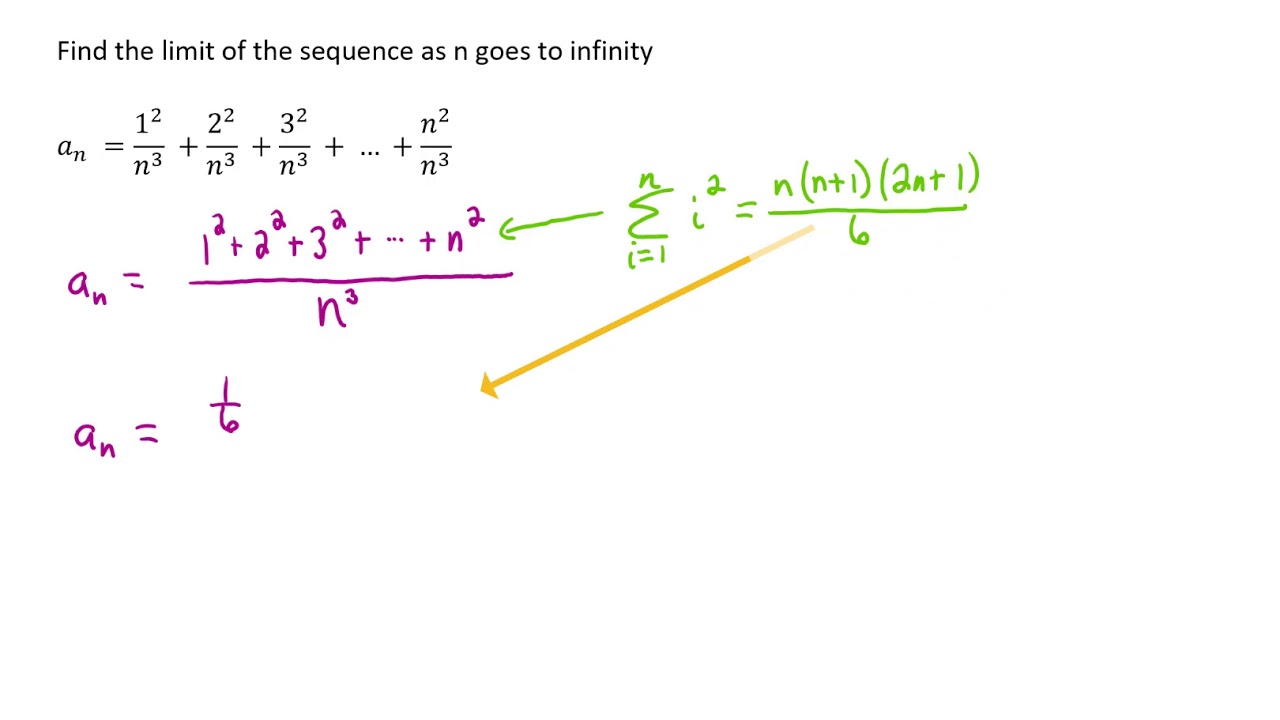



Find The Limit Of 1 N 3 2 2 N 3 3 2 N 3 N 2 N 3 As N Goes To Infinity Sequences 2 Youtube
I lim n n 3 n 2 n 1 n 3 n n 2 n 1 lim n 2 n 4 n 3 n 2 n n 2 n 1n 2 n 1 limn 2 n from MATH 142 at University of Wollongong Transcript Prove 1 2 3 n = (n(n1))/2 for n, n is a natural number Step 1 Let P(n) (the given statement)\ Let P(n) 1 2 3 n = (n(n1))/2 StepNếu limun = L lim u n = L thì lim√un 9 lim u n 9 có giá trị là bao nhiêu?




Answered S 1 Is N N 1 Convergent Divergent Check Bartleby




If A N 1 Frac 3 A N 2 A N 1 And A 1 1 Then What Is Lim Limits N To Infty Left Frac 4 3 Right N 3 A N Mathematics Stack Exchange
< n!2, we have 3n n!2 < 3n n!The denominator is (5 2 n) goes to 5, so the form goesGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!




Evaluate Lim N 1 N 1 1 N 2 1 2n Mathematics 1 Question Answer Collection




N 1 2 2 2 3 2 N 2n 3 Is Equal To
L'Hospital's Rule states that the limit of a quotient of functions is equal to the limit of the quotient of their derivatives lim n → ∞ n 2 n = lim n → ∞ d d n n d d n 2 n lim n → ∞ n 2 n = lim n → ∞ d d n n d d n 2 n Find the derivative of the numerator and denominator Tap for more stepsIt is easier to work with limits involving powers when the base is the sum of math1/math and something else To do this, factor out math3^n/math mathL=\displaystyle\lim_{n\to\infty}(3^n2^n)^{\frac{1}{2n}}/math math\implies L=\displSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more
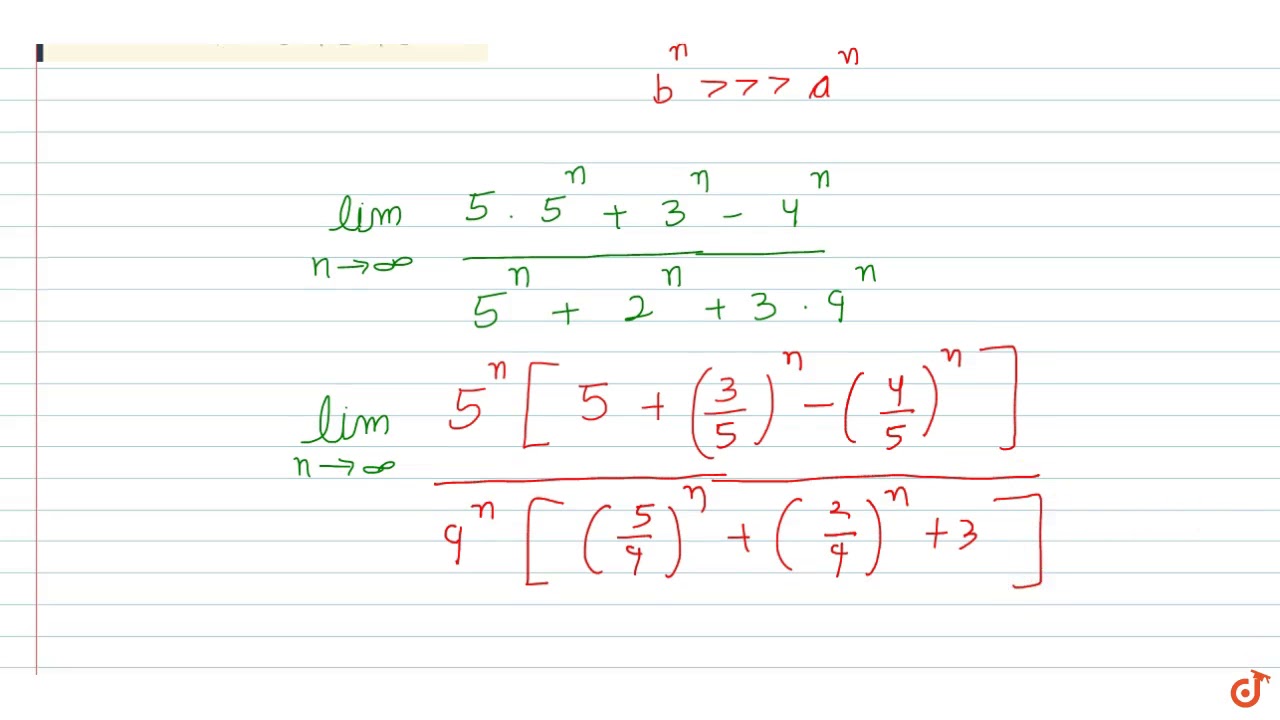



Lim N Gtoo 5 N 1 3 N 2 2n 5 N 2 N 3 2n 3 Youtube




Sheet 1 Mathematical Structures Teaching Mathematics
Lim n!1 2 = 2; Giới hạn đặc biệt lim √n = ∞ lim nk = ∞ (k ∈ Z ) lim qn = ∞ (q > 1) 2 Định lí a) Nếu lim un = ∞ thì lim 1 un = 0 b) Nếu lim un = a, lim vn = ± ∞ thì lim un vn = 0 c) Nếu lim un = a ≠ 0, lim vn = 0 thì lim un vn = ± ∞Iz lny him n so I 112 lny lim hsro 2h buy lim nsx 2 buy Z e e y eT 1 feign it 3h by Lyin z I hy if lay I b g Life Zn bn It 3mi ee my Liz hcII lay s 11 1 him x 2 2 5 of slim 2 2 him xx 4x him 4 o by 1 en e ti m hr e re ex ten yze Isis




Solved Lim N Tends To Infinity 1 2 3 1 3 4 1 N N 1 Equals Brainly Com




Limits
Lim n!1 sin(n) n2 = 0 The last limit is a result of an application of the squeeze theorem, since we have the inequalities 1 n 2 sin(n) n 1 n2 Putting these results together, we conclude that (a n)1 n=1 is convergent, and its limit is equal to lim n!1 a n = 5 0 0 (2 0)(2 0) = 5 4Weekly Subscription $199 USD per week until cancelled Monthly Subscription $699 USD per month until cancelled Annual Subscription $2999 USD per year until cancelledLim N → ∞ 1 2 2 2 3 2 N 2 N 3 CBSE CBSE (Commerce) Class 11 Textbook Solutions 79 Important Solutions 14 Question Bank Solutions 6793 Concept Notes & Videos 3 Syllabus Advertisement Remove all ads Lim N → ∞ 1 2 2 2 3 2 N 2 N 3




A Limit Involving Binomial Coefficients Lim N To Infty 1 N Sum K 1 N 1 K N Choose K 1 K Frac12 Mathoverflow




Chapter 3 Cbu
Câu hỏi Biết \(\lim \frac{{{1^3} {2^3} {3^3} {n^3}}}{{{n^3} 1}} = \frac{a}{b}\left( {a,b \in N} \right)\) Giá trị của \(2{b^2} {a^2}\) làIIT JEE 12 Determinants 5 If the sum of n terms of an AP is given by S n = n 2 n, then the common difference of the AP is KCET 6 The locus represented by x y y z = 0 is KCET 18 Three Dimensional Geometry 7 If f (x) = sin − 1 ( 2 x 1 x 2), then f' ( 3) isNotice that if you allow splitting the limit into sum of limits you can arrange it to be any real number Indeed, take any x \in \mathbb{R} For k \in \{1, \ldots, n\} we have \displaystyle\lim_{n \to \infty} \frac{n}{n^2k} = 0 = \lim_{n\to\infty} \frac{x}{n}




Geneseo Math 222 01 Absolute Convergence



Math 414 Real Analysis Assignments
`=2/6=1/3` Vậy `lim\frac{1^22^23^2n^2}{n(n1)(n2)"=1/3` Leave an answer You must login or register to add a new answer Đăng Nhập Forget Remember Me Register;Converges and the comparison test implies that P n n!2 also converges 15 Applying the ratio test, we have limX1 n=1 n p n n2 converge or diverge Be sure to give a complete explanation Answer Since lim n!1 n p n= 1 as we discussed in class, a limit comparison to the series P 1 n2 is a natural lim n!1 n p n n2 1 n2 = lim n!1 n p n n2 n2 1 = lim n!1 n p n= 1 Therefore, since the series P 1 n2 converges, the Limit Comparison Test implies that the




The Value Of Lim X Oo 5 N 1 3 N 2 2n 5 N 2 N 3 2n 1



2
29 Applying the ratio test to X (2n)!xn 22n(n!)2 X anx n, we obtain ρ = limx (2n 2)(2n 1) 4(n 1)2 = x Thus P anxn converges absolutely if −1 < x < 1, and diverges if x > 1 or x < −1 In Exercise 36 of Section 93 it was shown that an ≥ 1 2n, so the given series definitelyHint the sine function (c) X∞ n=0 (−1)n 2nn!Hence $\lim(\frac{3n2}{n1})=3$ realanalysis limits convergencedivergence solutionverification Share Cite Follow edited 24 mins ago Dulce Deleche asked 13 hours ago Dulce Deleche Dulce Deleche 29 3 3 bronze badges New contributor Dulce Deleche is a new contributor to this site Take care in asking for clarification, commenting, and




3 Find 7t 1 Lim N Sin 3 Lim Arcsin G N 00 N 100 Cos N Homeworklib



2
Bài viết mới Đẹp Trai Là Số Một – Lục Mang Tinh;Answer to determine the following limits (1) lim n>?Lim(√n 10−√n) lim ( n 10 − n) có giá trị là bao nhiêu?




Find The Limit Of Frac N N 3 1 Frac 2n N 3 2 Dots Frac N Cdot N N 3 N Mathematics Stack Exchange




Pdf Infinite Series Pedro H Arinelli Barbosa Academia Edu
Limx → ∞ ( 2x3 − 2x2 x − 3 x3 2x2 − x 1 ) Go!Tính giới hạn lim n(n1) A 0 B 1 C 3/2 D Không có giới hạnĐặt Một Câu Hỏi Bạn Muốn Tìm Gì?




Let X N N 3 N For N 1 2 3 Then Lim N Chegg Com




ลำด บและอน กรม
Active 3 years, 4 months ago Viewed 3k times 1 I'm a beginner in demonstrations and I'm trying to prove that 2 < lim n → ∞(1 1 n)n < 3 I proved 2 < lim n → ∞(1 1 n)n, by Newton's binomial, but can't prove that lim n → ∞(1 1 n)n < 3 Can you give me a light?Z2n Solution (a) X= lim 3n 2n = lim 2 3 n= 2 3 limn= 1 Example 326 lim 5n3 32n 1 2n4 5n2 2 = lim 5n 2n4 = lim 5 2n = 5 2 lim 1 n = 0 Example 327 lim 2n3 n2 2n 1 n3 10n2 5 = lim 2n3 n3 = lim2 = 2 433 More Theorems on Limits In example 304 , we used an approximation to simplify the problem a little bit In this particular example, the approximation was




6 1 3 Areas As Limits Of Riemann Sums




Chapter 1
Solve limits stepbystep \square!Nếu limun = L lim u n = L thì lim 1 3√un8 lim 1 u n 8 3 có giá trị là baoLim_(n>oo)(123*n)/(n^2) Updated On 39 To keep watching this video solution for FREE, Download our App Join the 2 Crores Student community now!
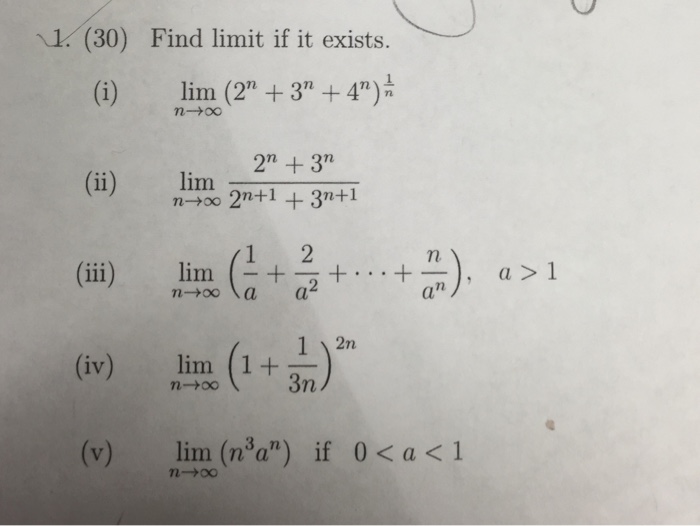



Find Limit If It Exists I Lim N Rightarrow Chegg Com



2
X → A lim 4 9 8 x x 2 (1 x 2) 1 / 3 − (1 − 2 x) 1 / 4 is equal to View solution The value of 3 2 4 3 8 1 3 − 1 9 2 3 3 7 5 isNow, applying the ratio test to the series P 3n n!, we obtain lim n→∞ 3n1 (n1)!Tính giới hạn limn(2n1) A1/2 B 0 C 2/3 D 2



2




Determine If The Sequence Frac 3 N N 3 1 Converges Or Diverges Mathematics Stack Exchange
Example 31A Show lim n→∞ n−1 n1 = 1 , directly from definition 31 Solution According to definition 31, we must show (2) given ǫ > 0, n−1 n1 ≈ ǫ 1 for n ≫ 1 We begin by examining the size of the difference, and simplifying it ¯ ¯ ¯ ¯ n−1 n1 − 1 ¯ ¯ ¯ ¯ = ¯ ¯ ¯ ¯ −2 n1 ¯ ¯ ¯ ¯ = 2 n1 The value of lim (1^2 2^2 3^2 n^2)(1^3 2^3 n^3)/1^6 2^6 n^6 where lim (x→ ∞) asked in Mathematics by Juhy (631k points) integral calculus;Now let us multiply and divide by the heighest power n^2 ==> lim (1 1/n)/ 2 (1 3/n 1/n^2) when n > inf ==> lim = (10)/2 (10 0) = 1/2 Then the limit = 1/2 Approved by eNotes Editorial



1




The Limit When N Tends To Infinity Of The Series Frac Sqrt N Sqrt N 3 Frac Sqrt
X1 n=1 n p n n2 converge or diverge Be sure to give a complete explanation Answer Since lim n!1 n p n= 1 as we discussed in class, a limit comparison to the series P 1 n2 is a natural lim n!1 n p n n2 1 n2 = lim n!1 n p n n2 n2 1 = lim n!1 n p n= 1 Therefore, since the series P 1 n2 converges, the Limit Comparison Test implies that the Thanks The standard method to find the limit of rational functions is to factor out the highest power of n both from numerator and denominator n 2 ( 3 1 / n 1 / n 2) n 3 ( 5 − 2 / n 2 / n 2) Simplify by n^2, and take the limit separately for each terms You are left with the limit of 3/ (5n) ehildWelcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries







2
Lim N → ∞ N 2 1 2 3 N CBSE CBSE (Commerce) Class 11 Textbook Solutions 79 Important Solutions 14 Question Bank Solutions 6793 Concept Notes & Videos 3 Syllabus Advertisement Remove all ads Lim N → ∞ N 2 1 2 3 N lim(n →∞) (3^n 5^n 7^n)^1/n is equal to (A) e^3 (B) e^5 asked in Limit, continuity and differentiability by Vikky01 ( 418k points) limits Diverges by the Limit Comparison Test Due to the simplicity of the series, we can use the Limit Comparison Test, which tells us if we have some positive sequence b_n and we know the convergence or divergence of sumb_n, then if c=lim_(n>oo)a_n/b_n>0 ne oo, then both series either converge or diverge Here, a_n=n^2/(n^31) For the comparison sequence, we need one




N Lim 12 Lim N 1 Ta Rl 1 2 3 N Lim R Lim Using The Ratio Test Test Meme On Me Me




Exercise 02 Studocu
(1)^n / (n^21) (2)lim n>?Let's factorize the numerator and denominators Numerator will be math(2–1)(2^221)(3–1)(3^231)(n1)(n^2n1) = (1*7)(2*13)(3*21)((n1)*(n^2n1One the one hand, lim(2n4) = 1, and, on the other hand, lim(5n2) = 1 So we are with the form the form (1=1) which is not determined and makes the problem interesting Some algebraic manipulations give 2n 4 5n 2 = 2 4 n 5 2 n In this new form, the numerator (2 4 n) goes to 2;




Ism Et Chapter 8




The Value Of Lim N Oo 1 2 3 N N 2 N 2 Is A 1 B



2




Lim N Oo 1 N 2 N 1 3 N 2 N 1 1 2 2 2 3 2 N 2




Evaluate The Following Limit Lim N Oo 1 N 2 2 N 2 3 N




Lim X Tends To Infinity 1 2 3 N N 2 Maths Limits And Derivatives Meritnation Com



2
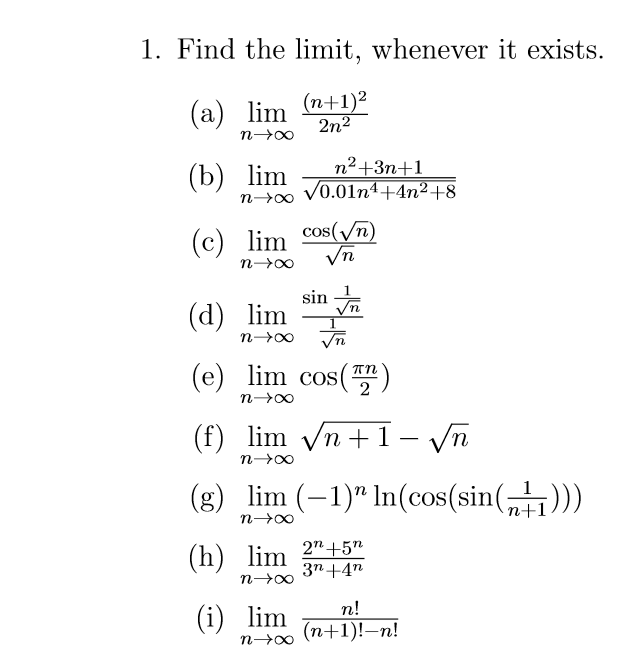



Find The Limit Whenever It Exists A Lim N Chegg Com
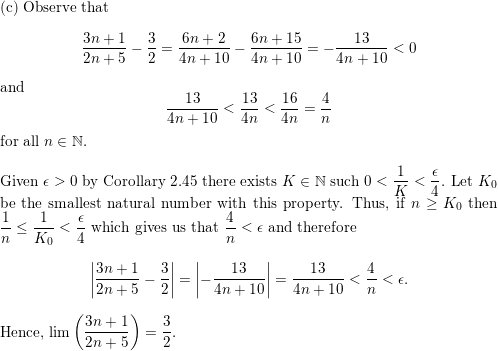



Use The Definition Of The Limit Of A Sequence To Establish The Following Limits A Math Lim Left Frac N N 2 1 Right 0 Math B Math Lim Left Frac 2 N N 1 Right 2 Math C Math Lim Left Frac 3 N 1 2 N 5 Right Math 3 2




Math 3210 3 Hw 24 Convergence Of Infinite Series




Assignment 1 Math 214 B1 1 Determine Whether The Given
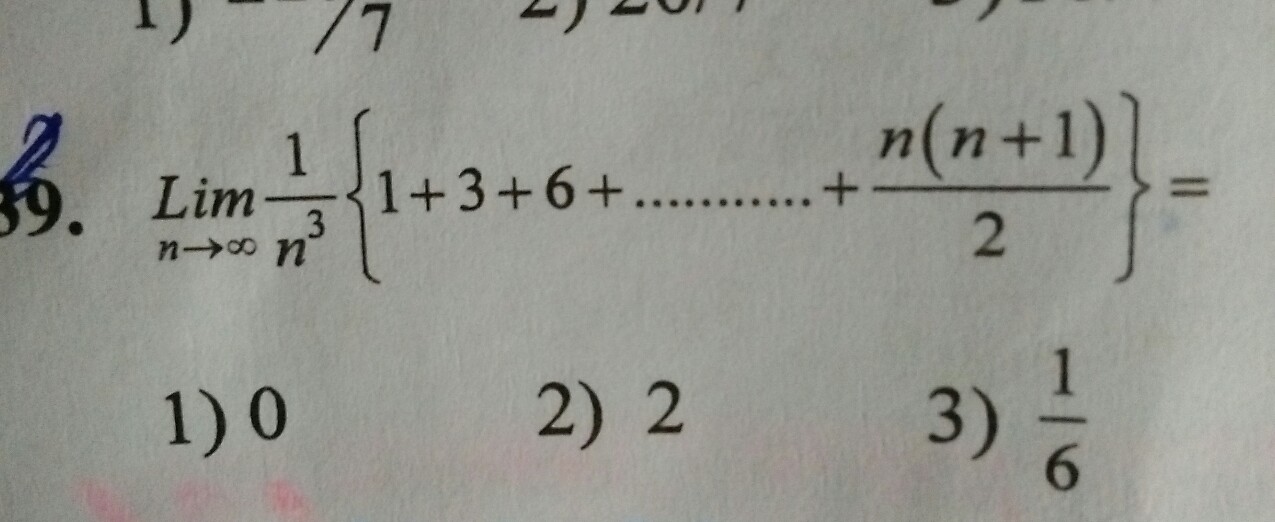



Lim N Infinity 1 N 3 1 3 6 N N 1 2




Calculus Find The Radius Of Convergence For 3n Online Presentation



Answered Use The Ratio Test To Determine Whether Bartleby




Number 4 As Clearly As Possible 1 Find The Limit Of The Following Sequences Find Lim Homeworklib




Lim N Tends To Infinity 1 2 2 2 N 2 N 4 Brainly In




Calculus Find The Radius Of Convergence For 3n Online Presentation




Calculus Find The Radius Of Convergence For 3n Online Presentation



Summation Formulas
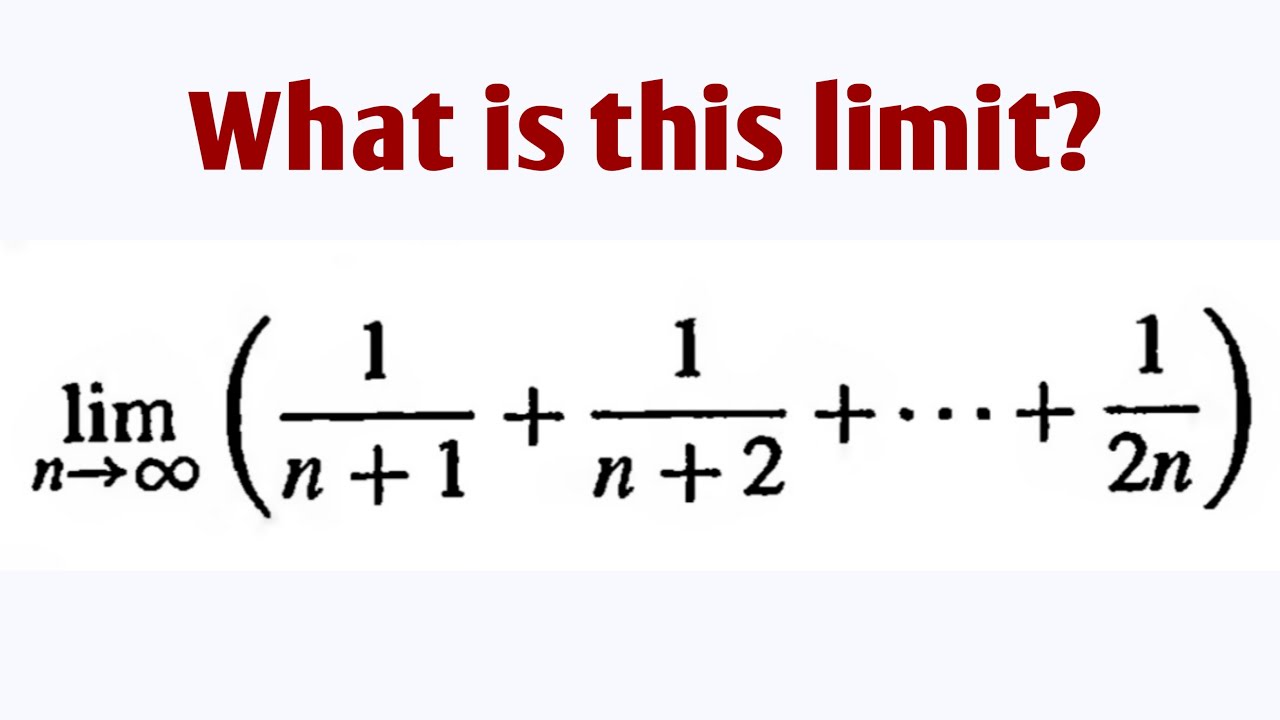



Lim 1 N 1 1 N 2 1 2n What Is This Limit Youtube




Show That Lim N Tends To Infinity 1 N 1 N 1 1 N 2 1 3n Log 3 Brainly In




Lim N Gtoo 1 2 3 4 5 6 2n Sqrt N 2 1 Sqrt 4n 2 1 1 1 3 2




1234n Formula
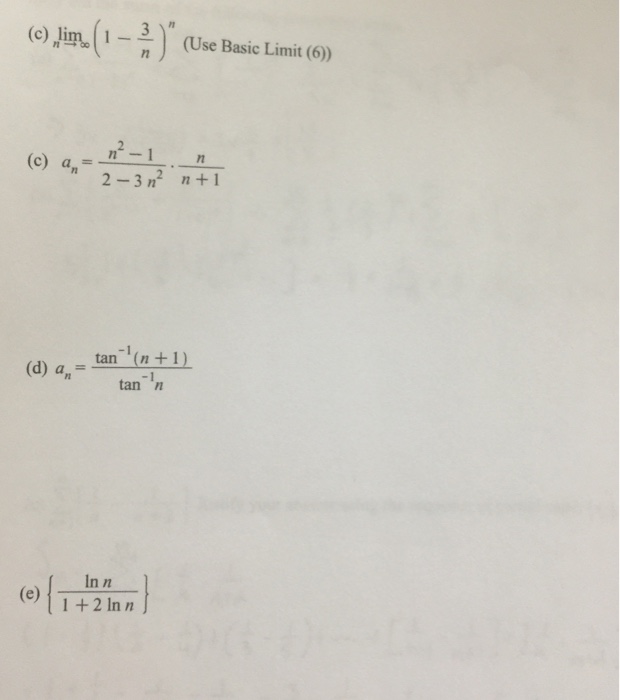



Lim N Rightarrow Infinity 1 3 N N Use Basic Limit Chegg Com




Limits Of Infinite Sequences Ppt Download



2



Tinh Giới Hạn Lim 2n 1 N 2 Lim 3n 2 1 N 2 4 Toan Học Lớp 11 Bai Tập Toan Học Lớp 11 Giải Bai Tập Toan



How To Evaluate The Limit Of Math Lim N To Infty Dfrac 1 N 1 Dfrac 1 N 2 Dots Dfrac 1 2n Math Quora




Evaluate Lim N 1 N 1 N 1 1 N 2 1 3n Youtube



2




Math 101 Homework 2 Solutions 1 Evaluate The Limits N




In Questions 1 8 Find The Limit Of The Sequence Sin N Cos N 2 37 N Sin N 3 4 Cos Rn 5 N Sin N O Cos N N 9 If




Answered N2 And Bn 1 Use The Limit Comparison Bartleby




6 1 3 Areas As Limits Of Riemann Sums



2




In Showing Integer Sum 1 2 3 N By L Hopital Rule Why They Take Lim As R Approaches To 1 In One Of Steps Why 1 Mathematics Stack Exchange



Math 414 Real Analysis Assignments




4 2 6 I 2 Points Find Lim 2 2 Points Recall Chegg Com




If A N 1 Frac 3 A N 2 A N 1 And A 1 1 Then What Is Lim Limits N To Infty Left Frac 4 3 Right N 3 A N Mathematics Stack Exchange




Section 10 6 Recall From Calculus Lim Lim Lim X Y X X X Kx K 1 Y Y Eekek Let Y Kx In The Previous Limit Ekek If Derivatives Ppt Download




1 1 Limits Exercises Ecalculus Csu Kaohsiung Taiwan



1 N Series




Sol 2 Functions And Mappings Complex Analysis



Limit Limit N N 1 N 2 3n N 2n 1 N Is Equal To Sarthaks Econnect Largest Online Education Community



What Is The Limit Of 2 N 1 3 N 1 2 N 3 N As N Tends To Infinity Quora




ลำด บและอน กรม




Log B Log A Log Bla N 1 N 2 N




Convergence Of The Series Sum Limits N 1 Infty Frac Left 1 Frac1n Right N 2 3n 2 2 E N Mathematics Stack Exchange



What Is The Value Of Lim N Infinity N N N 3n 3 4n 2 1 Quora



2




Definite Integral Evaluate Limn 1n N2 N 1 3 N2 N 2 3 Maths Integrals Meritnation Com
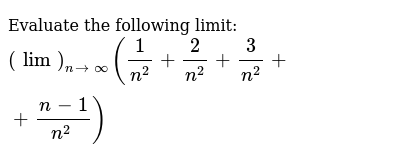



Evaluate The Following Limit Lim N Oo 1 N 2 2 N 2 3 N




2 3 6 1 2 Points Find Lim R4 2 2 Points Recall Chegg Com




Ex 7 8 4 Integrate X2 X Dx By Limit As A Sum Ex 7 8




Take For Granted That The Limit Lim 1 1 N N Chegg Com




Ism Et Chapter 8




N N 1 N 2 3nn 2n 1n Is Equal To



Lim N N 1 N 2 3n N 2n 1 N Is Equal To Sarthaks Econnect Largest Online Education Community




Evaluate Lim N 1 N 1 1 N 2 1 2n Youtube



Lim N Gtoo N 1 N 2 3n N 2n 1 N Is Equal To Youtube



2



Show That I Limn 1 2 3 N 3n 2 7n 2 1 6 Ii Limn 1 2 2 2 3n 2 1 2 5n 2n 3 9 25 Sarthaks Econnect Largest Online Education Community




Mth3101 Advanced Calculus Chapter 2



2




The Value Of Underset N To Oo Lim 2n 2 3n 1 5n 2 4n 2 Equals Youtube



What Is The Value Of Lim N Infinity N N N 3n 3 4n 2 1 Quora



What Is Lim 3 N 2 N 1 2n When N Tends To Infinity Quora



2



Solved Use The Limit Comparison Test To Check The Convergence Of The Series N 1 2 N 3 N 2 6 N 5 3 N 2 Explain What Series You Are Comparing Course Hero



Limit



0 件のコメント:
コメントを投稿