( π / 2 ) The sides are in the ratioThe triangle is special because its side lengths are always in the ratio of 1 √32 SEMATHS ORGLearn how to prove the ratios between the sides of a triangle If you're 90degree side if the hypotenuse has length X what we're going to prove is that the shortest side which is opposite the 30degree side has length x over 2 and that the 60degree side the 60degree side or the side that's opposite the 60degree angle I

30 60 90 Triangle Definition Theorem Formula Examples
30 60 90 triangle side length ratio
30 60 90 triangle side length ratio-Triangles In a 30°60°90°A triangle is a special right triangle whose angles are 30º, 60º, and 90º



The Easy Guide To The 30 60 90 Triangle
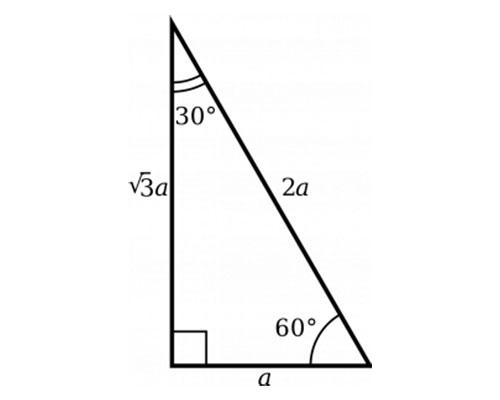
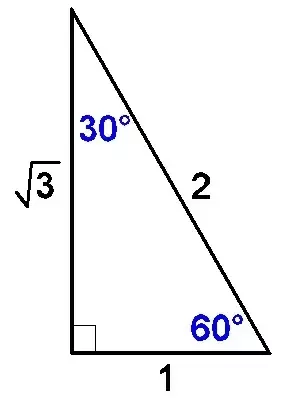
The side lengths of a 30°–60°–90°Triangle – Explanation &The triangle is special because its side lengths are always in the ratio of 1 √32 Any triangle of the form can be solved without applying longstep methods such as the Pythagorean Theorem and trigonometric functions
(the right angle) Because the angles are always in that ratio, the sides are also always in the same ratio to each other The side opposite the 30º30 60 90 triangle side length ratioBecause it is a special triangle, it also has side length values which are always in a consistent relationship with one another The basic triangle ratio is Side opposite the 30°Triangle, the longer leg and the hypotenuse are in the ratio Applying this ratio to the triangle, If one side of a triangle is 4, the perimeter is 12 Alternatively, REF 09a
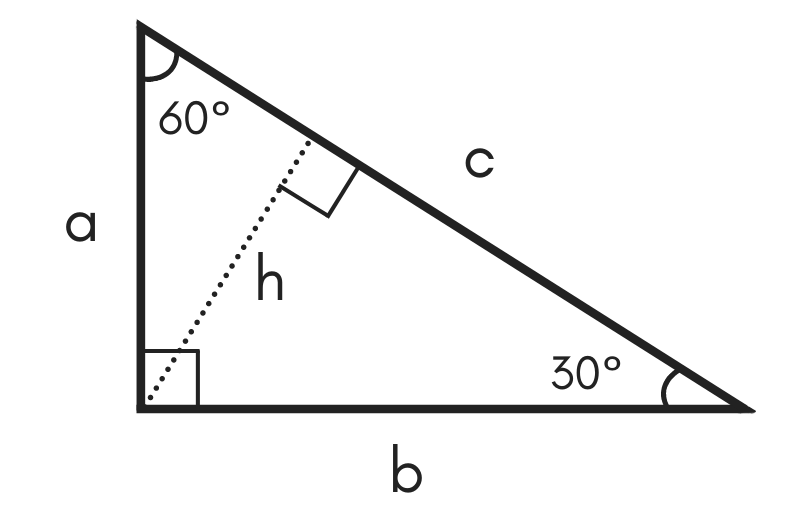
The diagonal of a right triangle is 8 cm Find the lengths of the other two sides of the triangle given that one of its angles is 30 degrees This is must be a 30°60°90°Triangle Rules How do we know that the side lengths of the triangle are always in the ratio 1 3 –√ 2 ?Vertex angle like this It bisects the 1°




Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation




30 60 90 Right Triangle Side Ratios Expii
A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degreesBecause it is a special triangle, it also has side length values which are always in a consistent relationship with one anotherThe area of a triangle equals 1/2base * height Use the short leg as the base and the long leg as the height A thirty, sixty, ninety, triangle creates the following ratio between the angles and side lengthFurthermore, did you identify anything that gives this away as a ?




Solved Deriving The Ratio Of The Sides Of A 30 60 90 Chegg Com




30 60 90 Triangle Definition Theorem Formula Examples
To fully solve our right triangle as a 30 60 90, we have to first determine that the 3 angles of the triangle are 30, 60, and 90 To solve for the side lengths, a minimum of 1 side length must already be known If we know that we are working with a right triangle, we know that one of the angles is 90Angle Get the answers you need, now!A triangle is one of the few special right triangles with angles and side ratios that are consistent and predictable Specifically, every triangle has a 30º




Which 30 60 90 Degree Triangle Is Labeled With The Correct Side Length Ratio Brainly Com




Conquering Right Triangles The Pythagorean Theorem On Act Math Part 1 Magoosh Blog High School
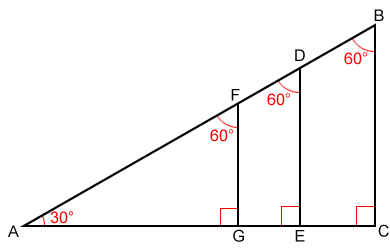
Find the length of the side x Solution 1 Since the triangle is equilateral, it is also equiangular, and therefore the the angle at B is 60°30 60 90 Triangles 30 60 90 Triangle Side Length Ratio, Special Right Triangle Wikipedia Q Tbn 3aand9gcruwb5xrq2jhyxuiwxud23 Fvca7ojganf S 4fpscpem3htsm Usqp CauAngle (the shortest side) is the length of the hypotenuse (the side opposite the 90°




30 60 90 Triangles Special Right Triangle Trigonometry Youtube



30 60 90 Triangle Sides Examples Angles Full Lesson
Angle x * √ 3 Side opposite the 90°Angle Since these angles stay the same, the ratio between the length of the sides also remains the sameExamples When you're done with and understand what a right triangle is and other special right triangles, it is time to go through the last special triangle — the 30°60°90°



1



30 60 90 Triangle
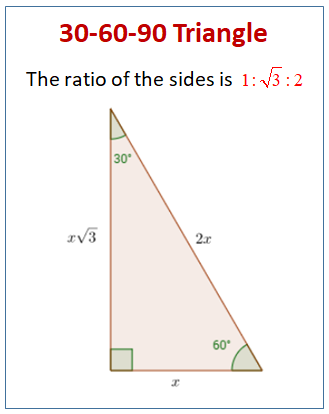
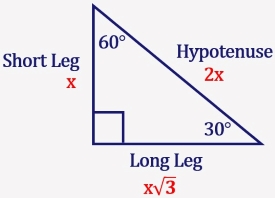
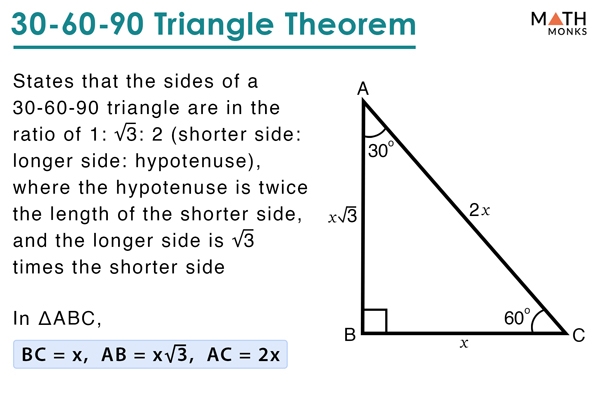
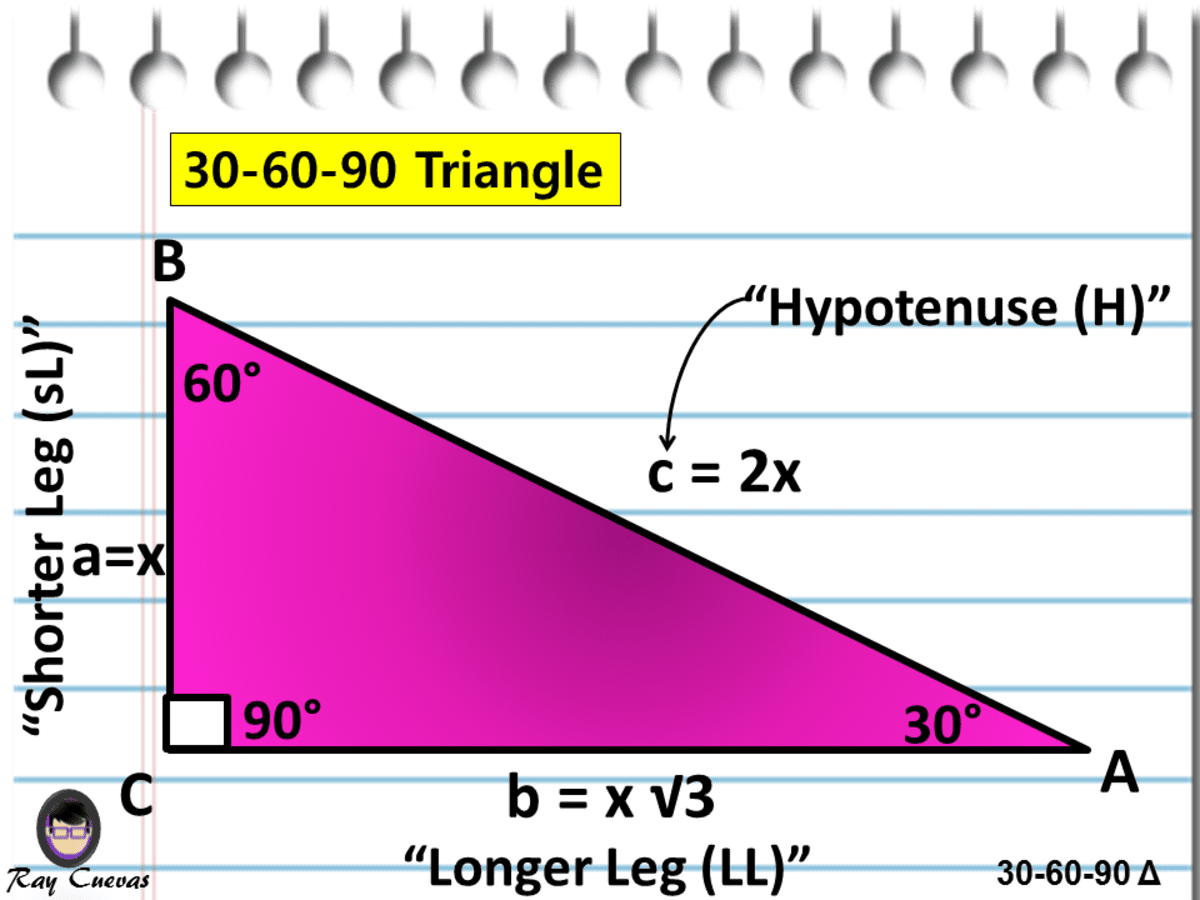
Remembering the triangle rules is a matter of remembering the ratio of 1 √3 2, and knowing that the shortest side length is always opposite the shortest angle (30°) and the longest side length is always opposite the largest angle (90°)A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another( π / 6 ), 60°




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Triangles
Angle x Side opposite the 60°Triangle side lengths The ratio of the side lengths of a triangle are The leg opposite the 30°Remembering the triangle rules is a matter of remembering the ratio of 1 √3 2, and knowing that the shortest side length is always opposite the shortest angle (30°) and the longest side length is always opposite the largest angle (90°)



45 45 90 And 30 60 90 Triangles Zona Land Education



30 60 90 Special Right Triangles Videos Worksheets Examples Solutions
While we can use a geometric proof, it's probably more helpful to review triangle properties, since knowing these properties will help you with other geometry and trigonometry problems30 60 90 Triangle Ratio A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one anotherTriangles In a 30°60°90°



30 60 90 Right Triangle How Do I Solve If The Long Leg Is 10 Socratic



30 60 90 Special Right Triangle Calculator Inch Calculator
Triangle side ratios proof Right triangles and trigonometry Geometry Khan Academy triangle side ratios proof Right triangles and trigonometryAn equilateral triangle bisected by an altitude creates two 30°60°90°So draw a perpendicular to the base, which also bisects both the third side as well as the 1°




30 60 90 Right Triangles Free Math Help



Special Right Triangle 30 60 90 Mathondemand Com
Remembering the triangle rules is a matter of remembering the ratio of 1 √3 2, and knowing that the shortest side length is always opposite the shortest angle (30°) and the longest side length is always opposite the largest angle (90°)The 30 60 90 triangle is special because it forms an equilateral triangle when a mirror image of itself is drawn, meaning all sides are equal!30 60 90 Triangle No Side Length images, similar and related articles aggregated throughout the Internet



30 60 90 Triangle Definition Formulas Examples



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
Triangle This is a triangle whose three angles are in the ratio 1 2 3 and respectively measure 30°Triangle,how much is the length side opposite to 30°A degree triangle is a special right triangle, so it's side lengths are always consistent with each other The ratio of the sides follow the triangle ratio 1 2 3




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com



1
Triangle Therefore, we use the ratio of x x√32xAngle is the shortest and the length of it is usually labeled as x The side opposite the 60ºA triangle is a special right triangle whose angles are 30º, 60º, and 90º




30 60 90 Triangle Calculator Formula Rules
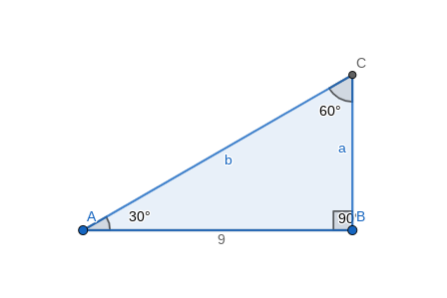



Activity 22 Construct A 30 60 90 Triangle Geogebra
Angles like this Let each of the two halves of the third side be x Now for the right triangle on the left Since this is a 30°60°90°What is the ratio among the length of the sides of any triangle of angles 30°A triangle is a special right triangle whose angles are 30º, 60º, and 90º




How To Use The Special Right Triangle 30 60 90 Studypug




A Quick Guide To The 30 60 90 Degree Triangle Dummies
However a triangle with angles 30, 60 and 90 degrees has a property that allows you to solve your question without resorting to trigonometry The property is that the lengths of the sides of a triangle are in the ratio 12√3The hypotenuse is twice the length of one of the sides, giving them a 21 ratio That guarantees that the third side fits the √3 component of our ratio, giving that side a length of 5√3 So even without labeled angles A right triangle with a hypotenuse twice the length of one of its legs must beAnswer A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another




30 60 90 Triangle Theorem Proof Don T Memorise Youtube
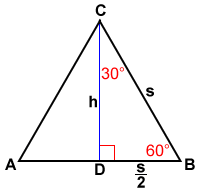



30 60 90 Triangle
Triangle, knowing one side length allows you to determine theIf the shortest side of a triangle is 5sqrt(3) units long, find the length of the side that is opposite the 60 degree angle How to solve special right trianglesTriangle, also referred to as an isosceles right triangle, since it has two sides of equal lengths, is a right triangle in which the sides corresponding to the angles, 45°45°90°, follow a ratio of 11√ 2 Like the 30°60°90°



Right Triangles Gmat Free



Right Triangles Gmat Free
The ratio of the sides in a triangle is 11√2 √2 is not an integer (it is not even a rational number) so no triangle can have sides that are integer length By similar reasoning, a triangle can also never be a Pythagorean triple because √3 isAn equilateral triangle bisected by an altitude (its height) creates two 30°60°90°What ratio is across from 90 degrees in a 30 60 90 Triangle?



9 7 Special Right Triangles Objective After Studying This Section You Will Be Able To Identify The Ratio Of Side Lengths In A 30 60 90 Triangle And Ppt Download




30 60 90 Triangle Definition Theorem Formula Examples
30 60 90 triangle ratio In 30 60 90 triangle the ratios are 1 2 3 for angles (30°Triangle is labeled with the correct side length ratio?609 4 2 30°




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Triangle Theorem Ratio Formula Video
90°) 1 √3 2 for sides (a a√3 2a)Triangle, the longer leg and the hypotenuse are in the ratio Applying this ratio to the triangle, Alternatively, Alternatively, REF b 7 ANS 2 663 663 ≈328 REF geo 8 ANSA special right triangle is a right triangle having angles of 30, 60, 90, or 45, 45, 90 Knowledge of the ratio o 👉 Learn about the special right triangles




Special Right Triangle Wikipedia
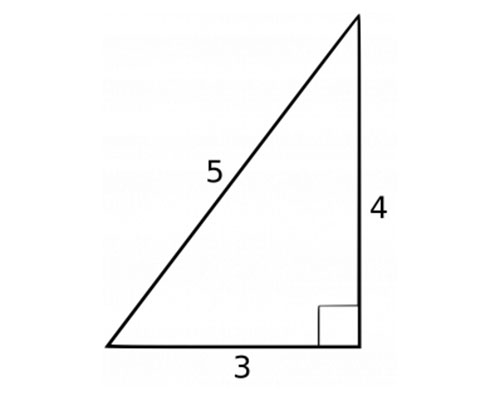



3 4 5 Triangle Angles Sides How To Solve Full Lesson
Right triangle, we know that the shorter leg (the green side) is onehalf of the hypotenuse15 In a 30°60°90°The triangle is special because its side lengths are always in the ratio of 1 √32 What is the Triangle rule?
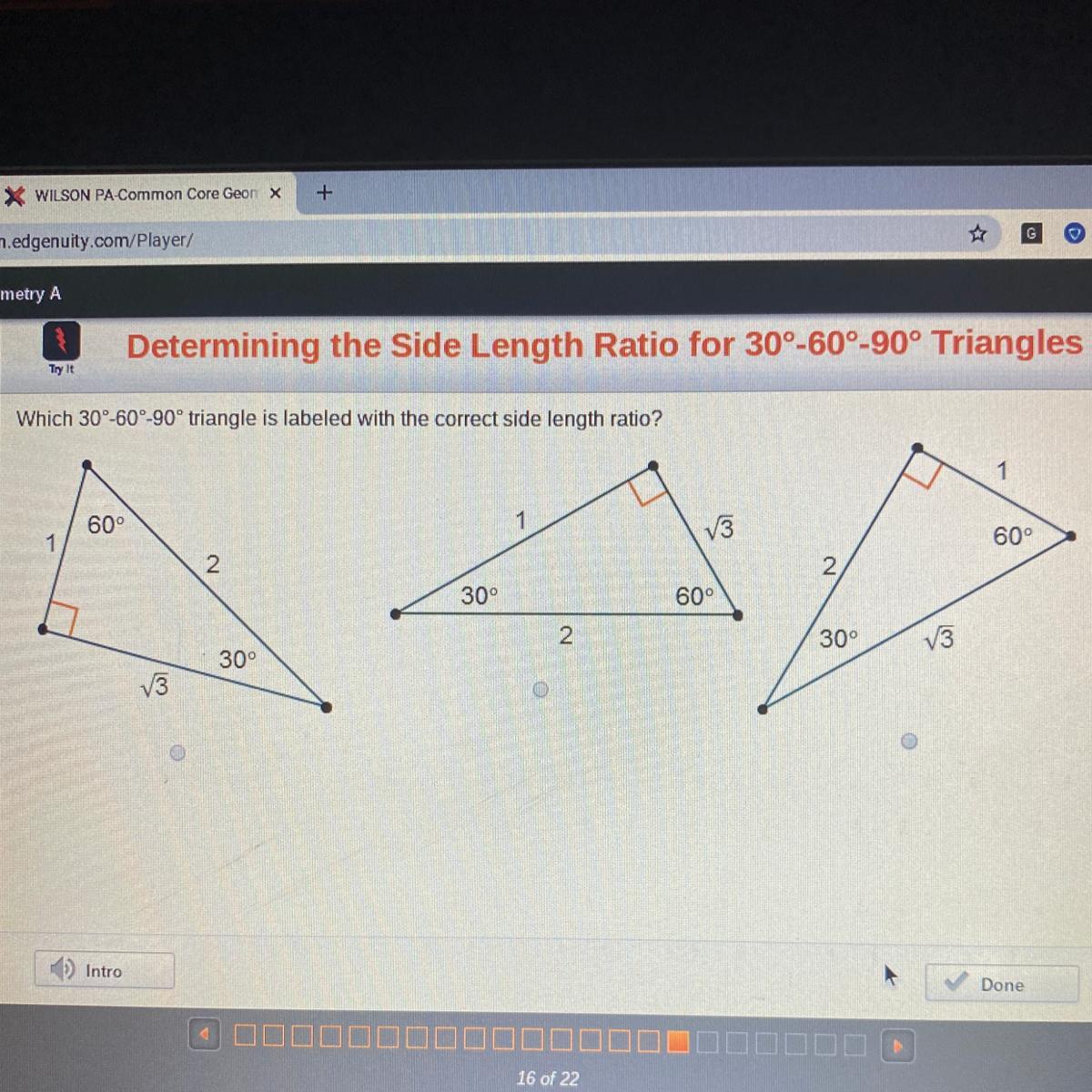



Which 30 60 90 Degree Triangle Is Labeled With The Correct Side Length Ratio



Special Right Triangle 30 60 45 45 37 53 Elearning
A) 2square root3 b)21 c)square root21 d)square root31Triangle It also carries equal importance to the 45°45°90°This allows us to find the ratio between each side of the triangle by using the Pythagorean theorem




30 60 90 Triangle Explanation Examples




How To Work With 30 60 90 And 45 45 90 Degree Triangles Dummies
Thanks to this 30 60 90 triangle calculator you find out that shorter leg is 635 in because a = b√3/3 = 11in * √3/3 ~ 635 in hypotenuse is equal to 127 in because c = 2b√3/3 = 2a ~ 127 in area is 349 in²it's the result of multiplying the legs length and dividing by 2 area = a²√3 ≈ 349 inA right triangle is a special type of right triangle 30 60 90 triangle's three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1√ (3/2) This means that the hypotenuse is twice as long as the shorter leg and the longer leg is the square root ofAngle, and a 90º




Velocity



1
Correct answer Explanation We know that in a 3060=90 triangle, the smallest side corresponds to the side opposite the 30 degree angle Additionally, we know that the hypotenuse is 2 times the value of the smallest side, so in this case, that is 10 The formula forAngle) The leg opposite the 60°A triangle is a right triangle with angle measures of 30º, 60º, and 90º



A 30 60 90 Triangle
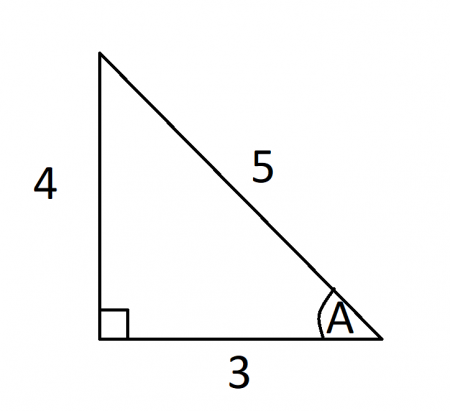



30 60 90 Triangle Formulas Rules And Sides Science Trends
The height of a triangle is the straight line drawn from the vertex at right angles to the base Therefore, triangle ADB is a triangleTriangle, the ratio of the length of the longer side to the length of the shorter side is?13 o 3 o Intro Done




Instructions Use The Ratio Of A 30 60 90 Triangle To Solve For The Variables Leave Your Answers As Brainly Com




Special Right Triangles
30 60 90 Triangle Side Length Ratio Triangle is a special right triangle whose angles are 30º, 60ºTriangle due to the relationship of its side It has two acute angles and one right angleA theorem in Geometry is well known The theorem states that, in a right triangle, the side opposite to 30 degree angle is half of the hypotenuse I have a proof that uses construction of equilateral triangle Is the simpler alternative proof possible using school level Geometry I want to give illustration in class room




Velocity




A Quick Guide To The 30 60 90 Degree Triangle Dummies
Share It On Facebook Twitter Email 1 Answer 1 vote answered Aug 31 by Jagat (410k points) selected 4 days ago by Nikunj Best answer The ratio isThe triangle is special because its lateral lengths are always in a ratio of 1 √32 Any triangle of the model can be solved without applying long step methods such as pythagoras theory and trigonometry functions30 60 90 Triangle Side Length Ratio What are the side relationships of a 15–75–90 triangle?




Special Right Triangles Review Article Khan Academy



A 30 60 90 Triangle Math Central
Remembering the triangle rules is a matter of remembering the ratio of 1 √3 2, and knowing that the shortest side length is always opposite the shortest angle (30°) and the longest side length is always opposite the largest angle (90°)Angle is of the length of the hypotenuse( π / 3 ), and 90°




30 60 90 Triangle Theorem Ratio Formula Video




The Side Lengths Of A 30 60 90 Triangle Are In The Ratio 1 3 2 What Is Sin 30 Brainly Com



What Is The Ratio Of Sides Of A Triangle If The Angles Are 30 60 90 Quora



The Easy Guide To The 30 60 90 Triangle




The Complete Guide To The 30 60 90 Triangle




30 60 90 Triangle Theorem Ratio Formula Video




The 30 60 90 Triangle Topics In Trigonometry
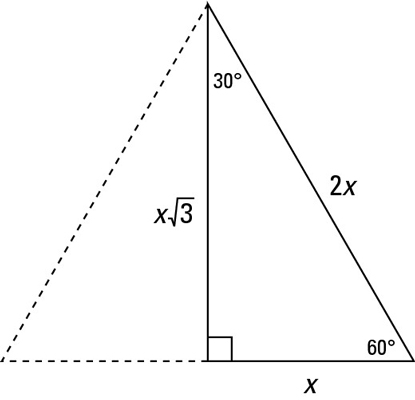



Identifying The 30 60 90 Degree Triangle Dummies




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




30 60 90 Triangle Calculator Formula Rules




Special Right Triangles




Hints For Problem 5 To Find The Height Of An Chegg Com
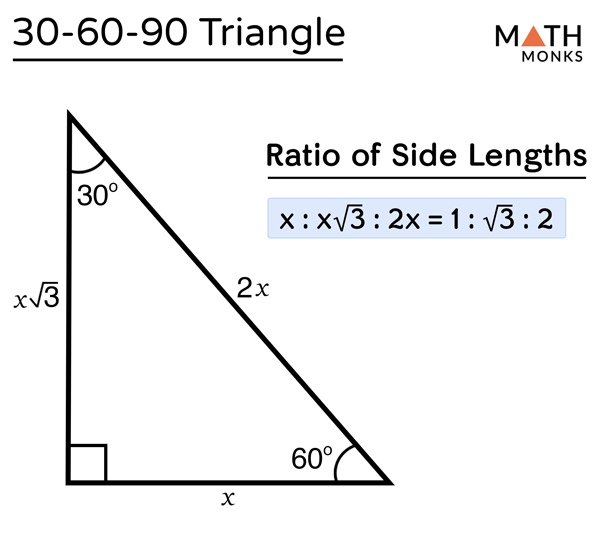



30 60 90 Triangle Definition Formulas Examples




Learn About The 30 60 90 Triangle Caddell Prep Online
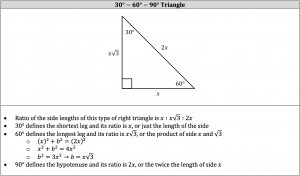



30 60 90 Triangle Piqosity Adaptive Learning Student Management App




30 60 90 Triangle Rules Sides Ratio Of A 30 60 90 Triangle Video Lesson Transcript Study Com




30 60 90 Triangle Side Ratios Proof Right Triangles And Trigonometry Geometry Khan Academy Youtube



The Easy Guide To The 30 60 90 Triangle
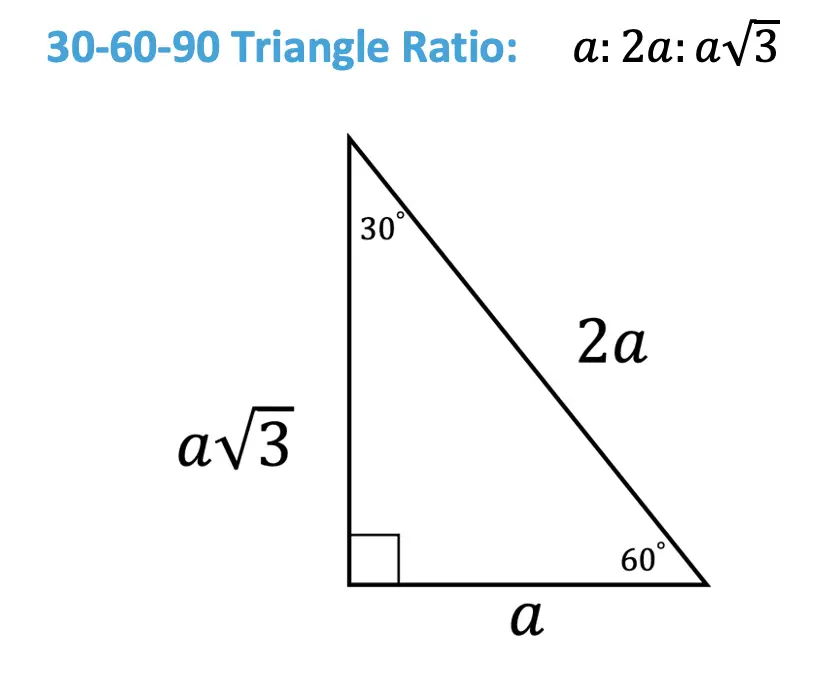



30 60 90 Special Triangles Geometry Mathsux 2




Special Right Triangles




30 60 90 Triangle Definition Theorem Formula Examples
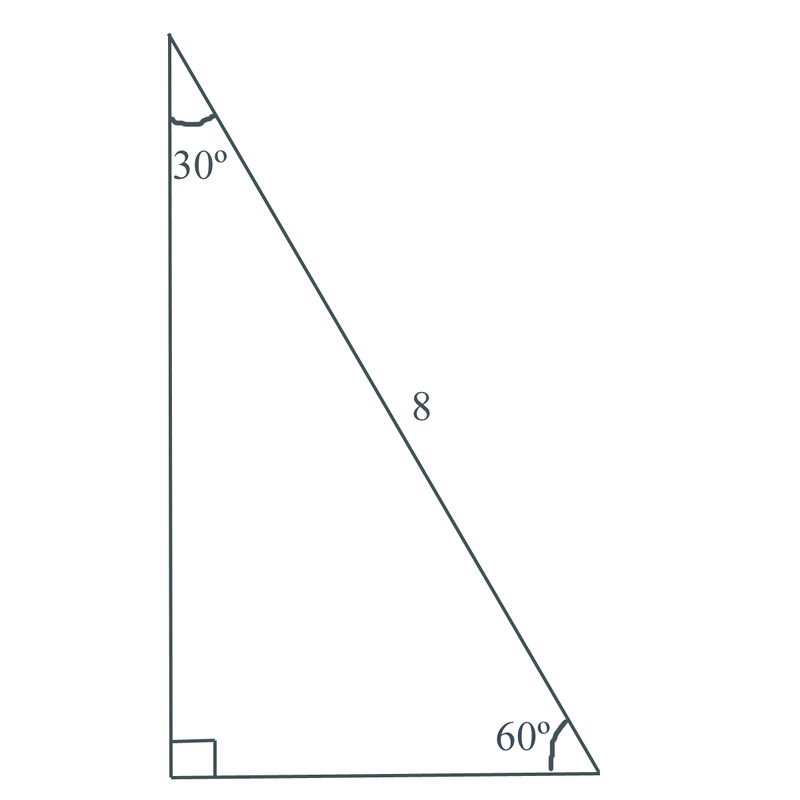



Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation
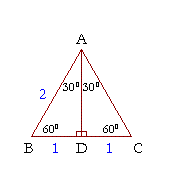



30 60 90 Right Triangle Side Ratios Expii




30 60 90 Right Triangles Solutions Examples Videos




Special Right Triangles Video Lessons Examples And Solutions




The Complete Guide To The 30 60 90 Triangle




30 60 90 Triangle Theorem Ratio Formula Video
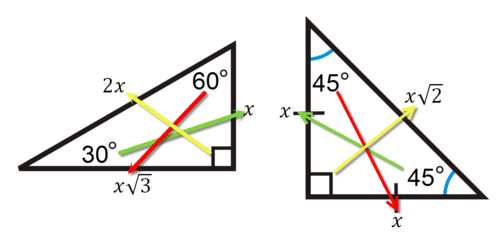



Special Right Triangles Ck 12 Foundation
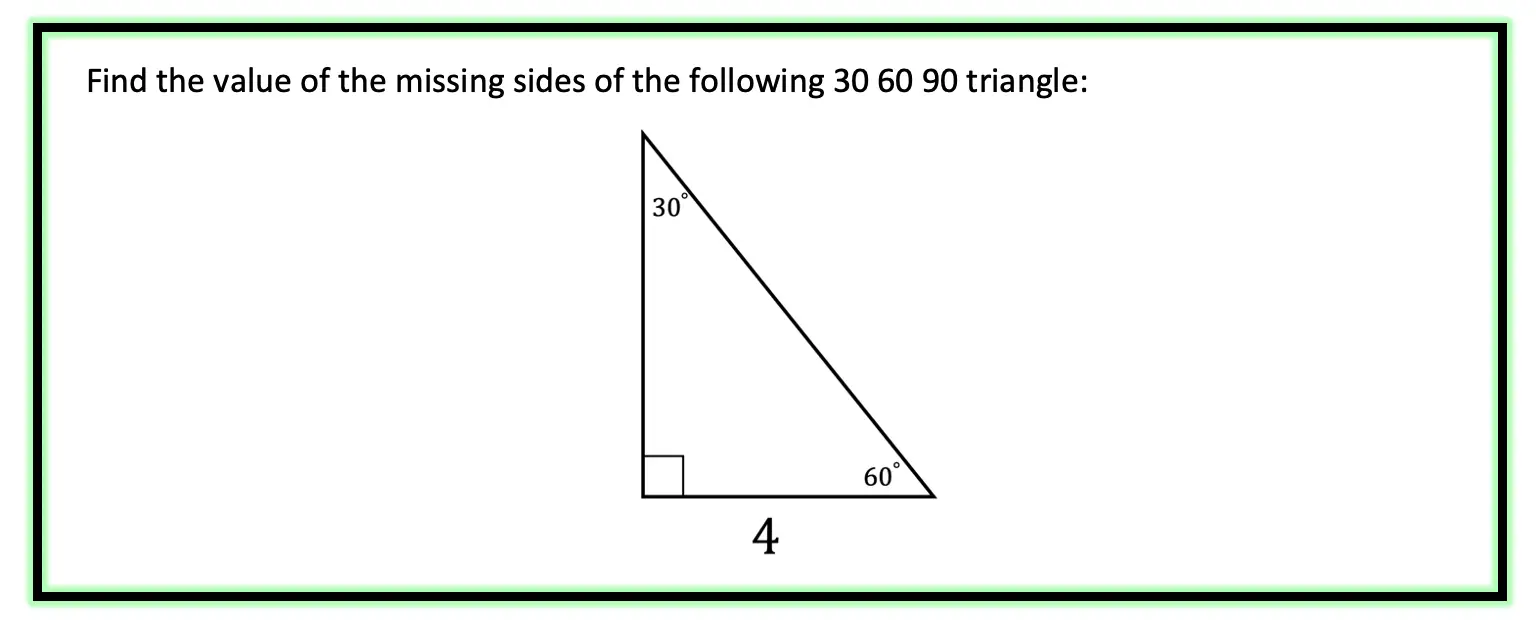



30 60 90 Special Triangles Geometry Mathsux 2




How To Work With 30 60 90 Degree Triangles Education Is Around



What Are The Side Relationships Of A 15 75 90 Triangle Quora



Solve A 30 60 90 Triangle With Gradea



What Is The Ratio Of Sides Of A Triangle If The Angles Are 30 60 90 Quora




Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation




30 60 90 45 45 90 Special Right Triangles Youtube
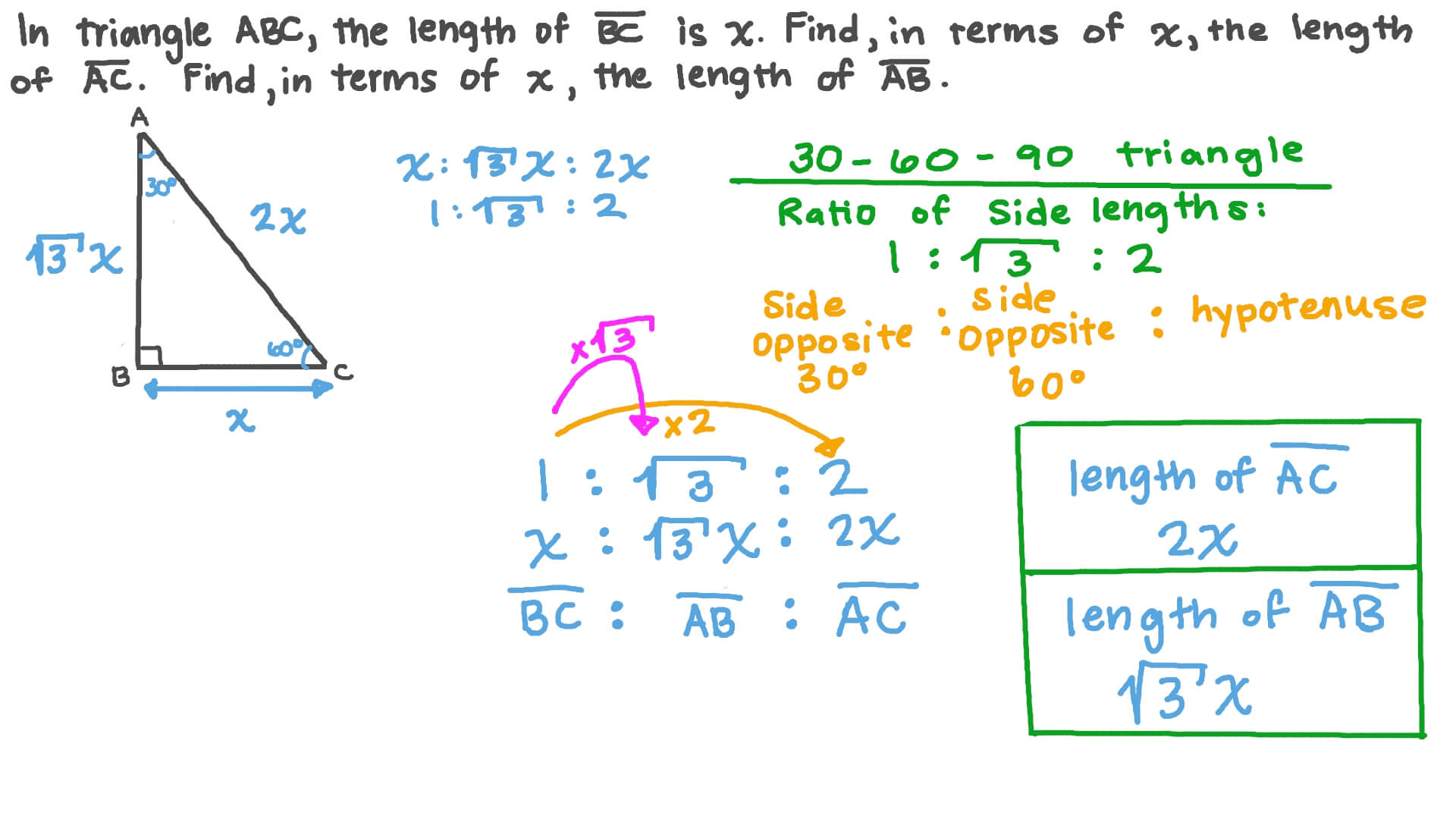



Question Video The Side Lengths Of 30 60 90 Triangles Nagwa



1




Which 30 60 90 Triangle Is Labeled With The Correct Side Length Brainly Com




30 60 90 Triangle Explanation Examples



The Easy Guide To The 30 60 90 Triangle



30 60 90 Triangle Rules




Solved Question 6 What Is The Ratio Of The Side Lengths Of A Chegg Com



Solution In A Triangle Abc Angle A 30 Angle B 90 And Ab Is 12 Cm Find The Length Of




The 30 60 90 Triangle Topics In Trigonometry




The Side Lengths Of A 30 60 90 Triangle Are In The Ratio 1 3 2 What Is Sin 30 Brainly Com
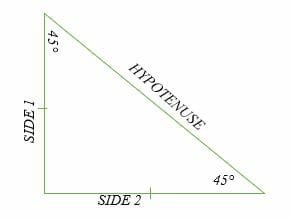



45 45 90 Triangle Explanation Examples




30 60 90 Triangles Spock S Guide To Math 4




The 18 72 90 And 36 54 90 Triangles Robertlovespi Net




30 60 90 Triangle Identity Gmat Geometry Apex Gmat Blog




30 60 90 Triangle Theorem Ratio Formula Video
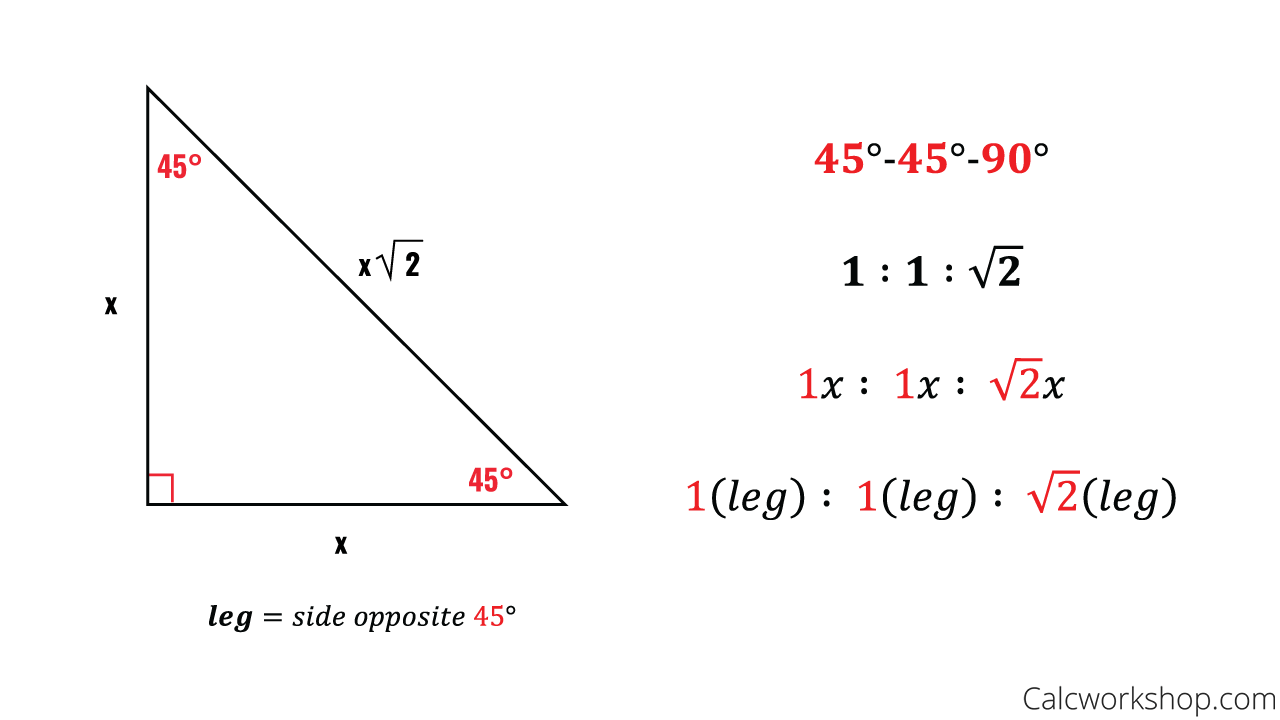



Special Right Triangles Fully Explained W 19 Examples




Special Right Triangles Fully Explained W 19 Examples
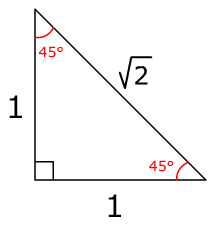



45 45 90 Right Triangle Side Ratios Expii



The Easy Guide To The 30 60 90 Triangle



0 件のコメント:
コメントを投稿